2つのゲーム間(例えばCSGOとOW)でセンシを合わせると言った時に、FOVの影響を考えず振り向きに必要なマウス移動距離で合わせてしまう人がいるが、これは間違ってるという話をする。その上で、どういう計算式によって合わせれば良いかという話をしようと思う。
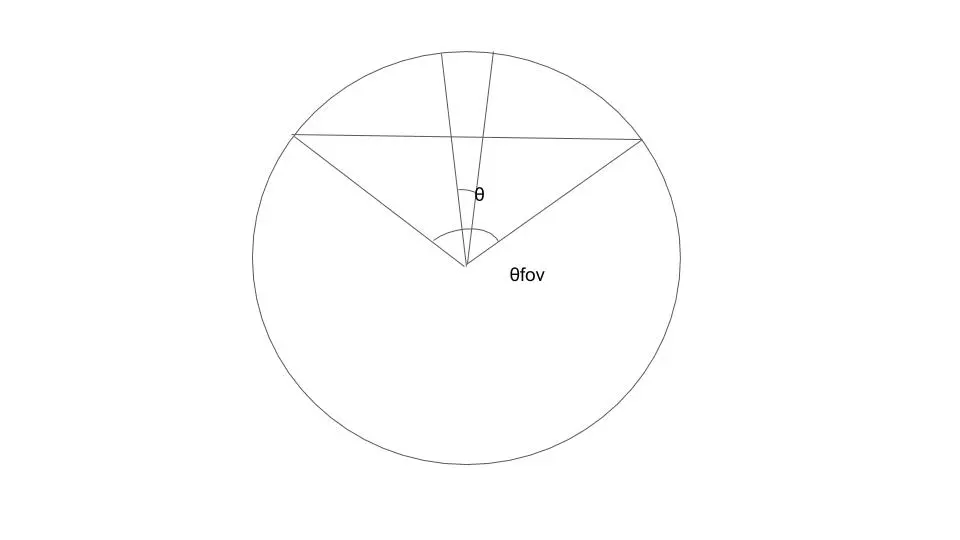
まずFOVとは何かというと「全方位360度のうち何度分を平面のディスプレイに投影しますか?」という数値だ。例えばCSGOでは106.26度、OWではデフォルトで103度となっている。
マウスをある距離動かした時に、どのくらいの角度を進むかは、振り向きの逆数で表すことが出来る。例えば振り向き3cmの人と30cmの人と比べると、1/3と1/30で後者の方が10倍角度が進まないということが言える。
例えばFOVの異なるゲーム間で振り向きを一緒にしてしまうと何が起こるかというと、FOVの小さい方では視界速度が速くなる。これは例えばPSAの結果に影響する。たとえば極端にFOV10度と100度のゲームがあったとしたら、これは自明だろう。(試しにOWのFOVを80度に下げてみると良い) だから、FOVの異なるゲームではFOVを意識した変換を行う必要がある。
ではどういう変換をすれば良いか?問題は円周には膨らみがあるのにディスプレイには膨らみがないことだ。これが誤差になるため、モニター上の距離を一致させるという方式では「では何度ないしは何パーセントの範囲でモニター距離を一致させるのか」で結果が変わってくる。これが、mouse-sensitivity.comのMonitor Distanceの設定でMatch Atというパラメータがある理由である。これは75%が推奨されているが、特に数理的な根拠があるわけではない。
そこで考えられたのが視界「距離」ではなくて「速度」(つまり微分)に着目するという方式で、これがmouse-sensitivity.comではViewspeedという形で実装されている。これについて説明する。
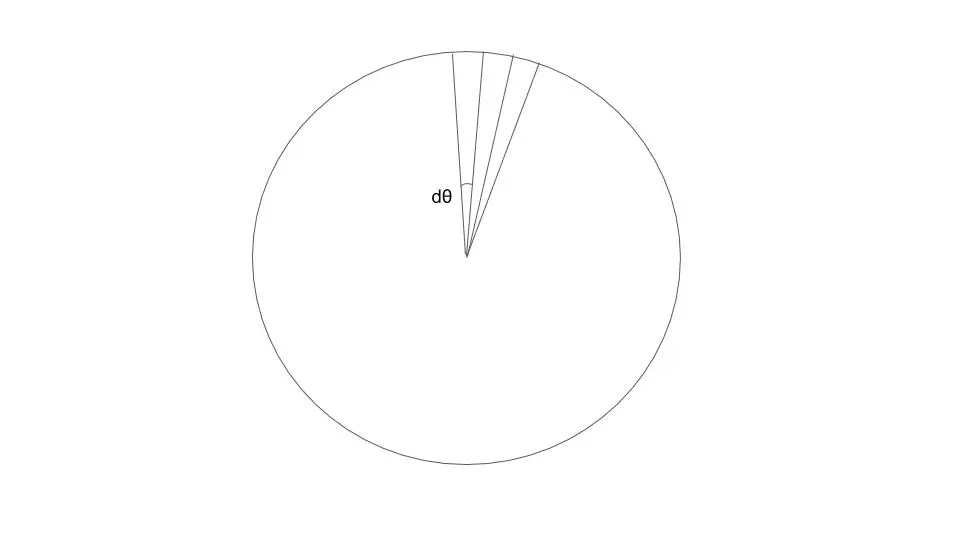
マウスをいくら振っても、視界は常に画面の真ん中にある。だから、大きな視界移動であっても、微小な視界移動の積み重ねと考えることが出来る。こう考えると、微小な視界移動について着目しても良いと分かる。(そもそも視界速度の定義はdθ/dt)
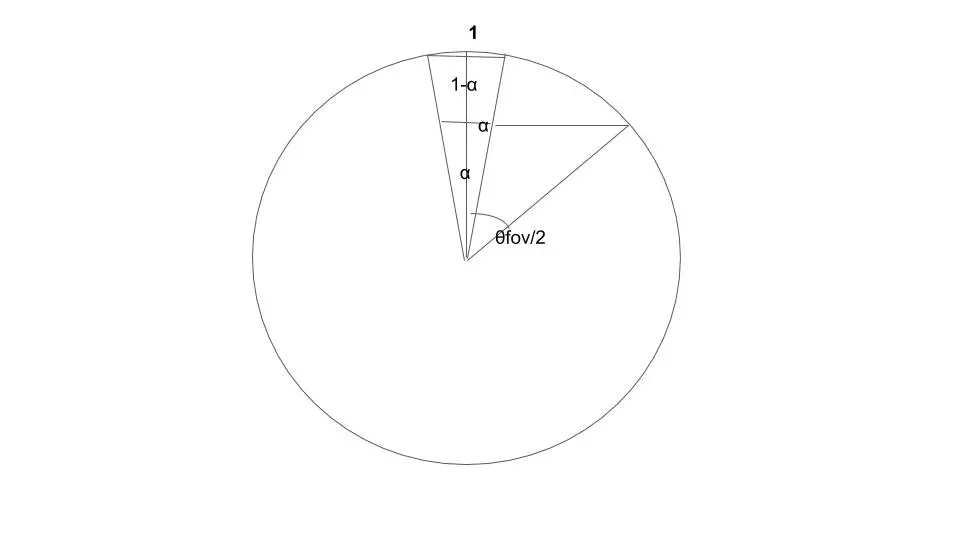
上の図でθが極めて微小な時、円の曲がりは無視することが出来る。つまり、円上の動き(つまり振り向きの逆数)とモニター上の距離の関係は、図にあるようにαで表すことが出来る。これより、α = cos(θfov/2)が言える。
今目指すことは、マウス上の微小移動距離に対してゲーム間でモニター上の微小移動距離のモニター上の割合を一致させることだから、前者を固定して議論しても良く,
1 / 振り向き1 * cos(θfov1 / 2) / sin(θfov1 / 2) = 1 / 振り向き2 * cos(θfov2 / 2) / sin(θfov2 / 2)
という関係が得られる。ここで添え字の1,2はゲーム1,2のこととする。
実際にmouse-sensitivity.comを使って確かめてみる。例えばScreaMが使ってる1000edpiというCSGOのセンシの場合、一周は41.5637cmである。
上の式は、
振り向き1 * tan(θfov1 / 2) = 振り向き2 * tan(θfov2 / 2)
となるから、
>>> 41.5637 * math.tan(106.2/2/180*math.pi) / math.tan(103.0/2/180*math.pi)
44.033463805534595
となって、OWでは3.93が適正と分かる。
しかし、これは、mouse-sensitivity.comのViewspeedとは違う。むしろただMonitor distanceで0%の場合を再計算しただけに相当する。Viewspeedはどうやらモニターのアス比や2D-3D変換も考慮に入れているようだが、おれとしてはFPSにおいてはほとんどのエイムはヘッドラインを保って水平方向に動かすだけであり、縦横を平等に扱うこと自体が間違ってると思うので、今回紹介した考え方に間違いがないのであれば、この方法でいきたいと思う。