この記事では、モニター距離一致はどうやって計算しているのかを自分で考えて、計算を行ってみる。その理由は、意図を計算式のレベルまで正しく理解することで、センシ変換についてより深い知見が得られると考えたからである。
mouse-sensitivity.comの計算結果と同じものが得られたので、一度まとめておく目的もある。
計算式
モニター距離を一致させるというのはどういうことか。これは言葉どおり、異なるFOV間で、同じモニター距離を動かすのに必要なマウス移動距離を等しくするという意味である。
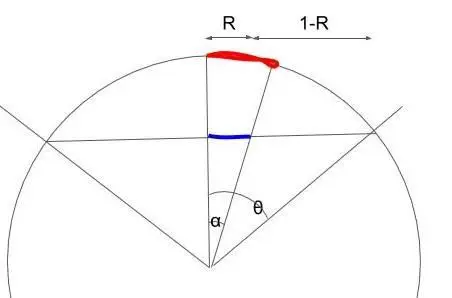
このような図を考える。便宜上、θは水平FOVの半角とする。Rは、どのくらいのモニター距離で一致させるかを意味する。例えばR=0.25であれば、25%のモニター距離で一致させるということを意味する。
モニター距離を一致させるとは、異なるθを持った2つの図があり、青部分の長さが等しい時に、同じ速度でマウスを動かしたとして、赤線を通る時間が同じということを意味している。
今、センシというのは角速度の逆数のことであるから、αを角速度で割ったものが一致すれば良いということになる。つまり、実はαがわかればよい。
比だけわかればよいので適当に直径を1とすると、青部分は、Rsinθである。また、円の中心から青線の左端までの距離はcosθである。つまり、α=arctan(Rtanθ)が成り立つ。2つのFOVにおけるαに添え字をつけてα0,α1と呼ぶこととする。
すると、α0 * sens0 = α1 * sens1が言える。なぜならば、上に述べたように、一致させるものは、α / (1/sens)だからである。
これより、sens1 = α0 * sens0 / α1が導けた。
Pythonによる実装とテスト
これをPythonで実装したものが以下となる。
import sys
import math
args = sys.argv
ratio = float(args[1])
fov0 = float(args[2]) * 0.5 * math.pi / 180
fov1 = float(args[3]) * 0.5 * math.pi / 180
sens0 = float(args[4])
alpha0 = math.atan(ratio * math.tan(fov0))
alpha1 = math.atan(ratio * math.tan(fov1))
sens1 = sens0 * alpha0 / alpha1
print(sens1)
何か適当な値でテストしてmouse-sensitivity.comとの一致を確かめてみる。
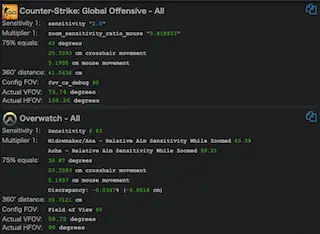
$ python3 mmx.py 0.75 106.26 90 41.5636
50.72858043985662
水平FOV106.26とFOV90の間で、75%のモニター距離一致を目的とした変換を行った場合、一周50.72cmとなれば良いことがわかる。やってみると、mouse-sensitivity.comでも50.71cm程度で、計算方法自体はおそらく正しいであろうということがわかる。
ちなみにRを極めて小さな0.000001のような値にすると、以下に書いた計算と同じになる。
【エイム数学】ゲーム間で視界速度を一致させる方法 - GAAブログ
私は基本的にはモニター距離0%でマッチさせるのがもっとも良いと考えていて、その理由は、長いフリックであっても結局人間にとっては、ざっくり合わせる+マイクロフリックの2段階に分解されているという考えがあるからである。この考えは私個人のものではなく、他にもこれを根拠にしてモニター距離0%を推奨している人がいる。関連した記事としては以下を読んでほしい。
ゲーム間センシはMonitor Distance 0%で合わせろ - GAAブログ
三角関数なんか社会人になったら使わないから意味ないという人がいる。面白くない冗談だな。三角関数がわからないとエイム変換を計算することが出来ないじゃないか。