In the game Overwatch, players can avoid at most three other players to be matched in your team. This is called avoid list but most players claims there should be more slots in the avoid list because there are more harmful players to avoid. It is also discussed in a official thread but no solid mathematical analysis is found on this issue. This is why I started to think about what if we have an infinite avoid list. Also, it is fun to solve real problem by the skill gained in competitive programming.
To begin with, let’s suppose we have N active players that are potentially chosen in a match making. The avoid list is considered as a directed graph with number of vertices N and number of edges N(N-1) where each edge(i,j) is colored black if player i avoids player j and white otherwise.
If the black edge is evenly distributed, this is an ideal situation but not practical because in practical a particular group of harmful (low-skilled, toxic, boosting, hacking, whatever) players is avoided by other players, but this assumption is a good starting point.
At some point there are K black edges in the graph and we chose an edge randomly then the probability that the edge is black is Pb = K/N(N-1).
Making a team is just choosing 6 members randomly so that any black edges are found in the group. Let’s call this the team is valid. Since team in Overwatch is 6 people there are 6(6-1) edges in the group. Thus, the probability that the team is valid is Pv = (1-Pb)^30.
Let’s draw the graph.
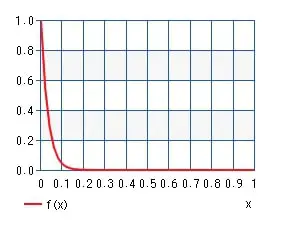
The x axis is Pb and y axis is Pv. When Pb is 0.01 or around which means players avoid 1 out of 100 people, there will be no bad effect to the queue time but when Pb closes to 0.1 (players avoid 1 out of 10 people) Pv becomes 0.04 this means queue time will be x25 compared to Pb=0 case.
Since it is easily imaginable players avoid other players in higher rate than Pb=0.01 but close to Pb=0.1 if there is an infinite avoid list. This is why Blizzard can not implement infinite avoid list. gg